Attention is All You Need

Notes on Attention is All You Need, i.e., the Transformer.

Encoder-Decoder Stacks

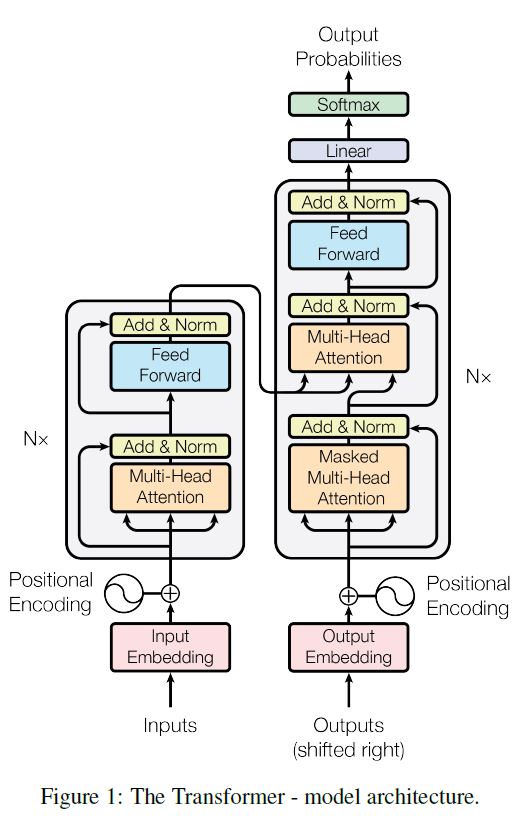
Encoder

A stack of $N=6$ identical layers; each layer has two sub-layers:

• A multi-head self-attention layer
• A simple, position-wise fully-connected feed-forward network (FC-FFN)

Decoder

A stack of $N=6$ identical layers; each layer has three sub-layers:

• A multi-head self-attention layer
  • Mask out subsequent positions
• A multi-head encoder-decoder attention layer
• A simple, position-wise fully connected feed-forward network (FC-FFN)

Residual Connection and Layer Norm

Empoly a residual connection around each of the sub-layers, followed by layer normalization. That is, the final output of each sub-layer is $\mathrm{LayerNorm} (x + \mathrm{SubLayer}(x))$, where $\mathrm{SubLayer}(x)$ is the output of a multi-head or FC-FFN layer.

Attention

Scaled dot-product attention, multi-head attention, self-attention.
See Attention in NLP.

Position-Wise Fully-Connected Feed-Forward Network

Apply a FC-FFN to each position separately and identically:

$$\mathrm{FFN}(x) = \mathrm{ReLU}\left( x W_1 + b_1 \right) W_2 + b_2$$

where $x \in \Bbb{R}^{d_{model}}$ is the vector on a certain position, $W_1 \in \Bbb{R}^{d_{model} \times d_{ff}}$ and $W_2 \in \Bbb{R}^{d_{ff} \times d_{model}}$ are trainable parameter matrices.

Embeddings and Softmax

Use learned embeddings to convert the source tokens and target tokens to vectors of dimension $d_{model}$.
Use learned transformation and softmax function to convert the decoder output to predicted next-token probabilities.

Positional Encodings

To make use of the order of sequence, add positional encodings to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimensions $d_{model}$ as the embeddings, so that they can be summed.

$$\begin{aligned} \mathrm{PE}(pos, 2i) &= \sin \left( \frac{pos}{10000^{2i/d_{model}}} \right) \\ \mathrm{PE}(pos, 2i+1) &= \cos \left( \frac{pos}{10000^{2i/d_{model}}} \right) \end{aligned}$$

where $pos$ is the position and $i$ is the dimension. That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from $2\pi$ to $10000 \cdot 2\pi$.
This positional encoding would allow the model to learn to attend by relative positions, since for any fixed offset $k$, $\mathrm{PE}_{pos+k}$ can be represented as a linear function of $\mathrm{PE}_{pos}$.

$$\begin{aligned} \mathrm{PE}(pos+k, 2i) &= \sin \left( \frac{pos+k}{10000^{2i/d_{model}}} \right) \\ &= \sin \left( \frac{pos}{10000^{2i/d_{model}}} \right) \cos \left( \frac{k}{10000^{2i/d_{model}}} \right) + \cos \left( \frac{pos}{10000^{2i/d_{model}}} \right) \sin \left( \frac{k}{10000^{2i/d_{model}}} \right) \\ &= \mathrm{PE}(pos, 2i) \cos \left( \frac{k}{10000^{2i/d_{model}}} \right) + \mathrm{PE}(pos, 2i+1) \sin \left( \frac{k}{10000^{2i/d_{model}}} \right) \end{aligned}$$