Attention in NLP

This blog briefly reviews the attention mechanisms in NLP.

The Encoder-Decoder Framework

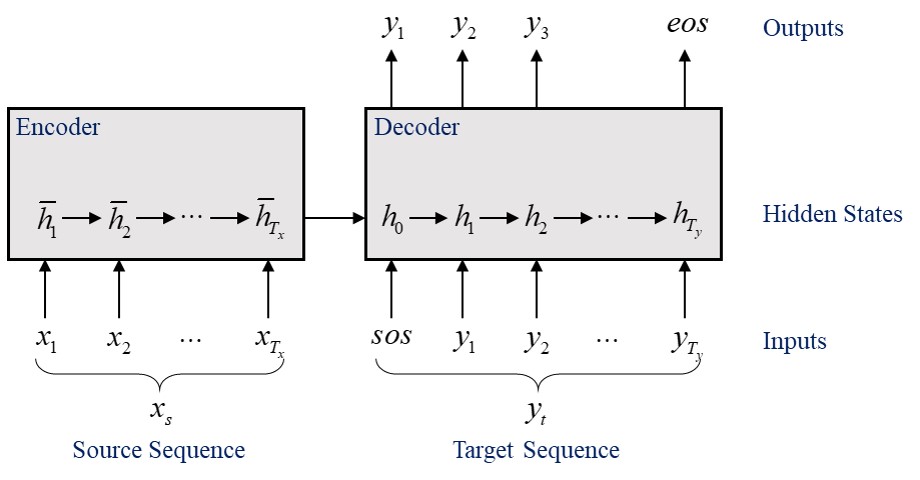
In the Encoder-Decoder framework, an encoder reads the source sentence, a sequence of vectors $x=\left( x_1, \cdots, x_{T_x} \right)$, into a fixed-length context vector $c$.

$$\begin{aligned} \bar{h}_s &= f \left( x_s, \bar{h}_{s-1} \right) \\ c &= q \left( \bar{h}_1, \cdots, \bar{h}_{T_x} \right) \end{aligned}$$

where $\bar{h}_s$ is the encoder’s hidden state at time $s$. $f$ and $q$ are some nonlinear functions. For example, one may use:

$$\begin{aligned} f &= \mathrm{LSTM} \\ q \left( \bar{h}_1, \cdots, \bar{h}_{T_x} \right) &= \bar{h}_{T_x} \end{aligned}$$

The decoder is often trained to predict the next word $y_t$ given the context vector $c$ and all the previous predicted words $\left\{ y_1, \cdots, y_{t-1} \right\}$. In other words, the decoder defines a probability over the translation $y=\left( y_1, \cdots, y_{T_y} \right)$ by decomposing the joint probability into the ordered conditional probabilities.

$$p(y) = \prod_{t=1}^{T_y} p\left( y_t | y_1, \cdots, y_{t-1}, c \right)$$

With an RNN, each conditional probability is modeled as

$$p\left( y_t | y_1, \cdots, y_{t-1}, c \right) = g\left( y_{t-1}, h_t, c \right)$$

where $g$ is a nonlinear function. $h_t$ is the decoder’s hidden state at time $t$.

Learning to Align and Translate

Bahdanau, D., Cho, K. and Bengio, Y., 2014. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.

Define each conditional probability as

$$p\left( y_t | y_1, \cdots, y_{t-1}, x \right) = g\left( y_{t-1}, h_t, c_t \right)$$

where $h_t$ is the decoder’s hidden state at time $t$, computed by

$$h_t = f\left( h_{t-1}, y_{t-1}, c_t \right)$$

Note that here the probability is conditioned on a distinct context vector $c_t$ for each target word $y_t$.
The context vector $c_t$ depends on a sequence of annotations $\left( \bar{h}_1, \cdots, \bar{h}_{T_x} \right)$ to which the encoder maps the source sentence. Each annotation $\bar{h}_s$ contains information about the whole source sequence with a strong focus on the parts surrounding the $s$-th word. For example, the annotations can be hidden states from a bidirectional RNN.
The context vector $c_t$ is computed as a weighted sum of these annotations:

$$c_t = \sum_{s=1}^{T_x} \alpha_{st} \bar{h}_s$$

The weight $\alpha_{st}$ of each annotation $\bar{h}_s$ is computed by:

$$\alpha_{st} = \frac{\exp(e_{st})}{\sum_{s'=1}^{T_x} \exp(e_{s't})}$$

where

$$e_{st} = \mathrm{score} \left( \bar{h}_s, h_{t-1} \right)$$

is an alignment model which scores how well the source words around position $s$ and the target word at position $t$ match. The score is based on the decoder’s hidden state $h_{t-1}$ and the encoder’s annotation $\bar{h}_s$.
The probability $\alpha_{st}$, or its associated energy $e_{st}$, reflects the importance of the annotation $\bar{h}_s$ with respect to the previous hidden state $h_{t-1}$ in deciding the next state $h_t$ and generating $y_t$. Intuitively, this implements an attention mechanism in the decoder.
The implement of the alignment model is

$$\mathrm{score} \left( \bar{h}_s, h_{t-1} \right) = v_a^\top \tanh \left( W_a \left[ \bar{h}_s; h_{t-1} \right] \right)$$

where $W_a$ and $v_a$ are trainable weights.

Global and Local Attetions

Luong, M.T., Pham, H. and Manning, C.D., 2015. Effective approaches to attention-based neural machine translation. arXiv preprint arXiv:1508.04025.

Global Attention

Very similar to Bahdanau et al. (2015).
The idea of global attention is to consider all the encoder’s hidden states when deriving the context vector $c_t$. The alignment vector $\alpha_t$, whose size equals the length on the source side, is:

$$\begin{aligned} \alpha_{st} &= \mathrm{align} \left( \bar{h}_s, h_t \right) \\ &= \frac{\exp \left( \mathrm{score} \left( \bar{h}_s, h_t \right) \right)}{\sum_{s'=1}^{T_x} \exp \left( \mathrm{score} \left( \bar{h}_{s'}, h_t \right) \right)} \end{aligned}$$

where $\mathrm{score}$ is the alignment function, which may have four alternatives:

$$\mathrm{score} \left( \bar{h}_s, h_t \right) = \begin{cases} \bar{h}_s^\top h_t, &\text{Dot product} \\ \bar{h}_s^\top W_a h_t, &\text{General product} \\ v_a^\top \tanh \left( W_a \left[ \bar{h}_s; h_t \right] \right), &\text{Concat} \\ \text{The } s\text{-th element of } W_a h_t, &\text{Location based} \end{cases}$$

where the location-based attention is computed sorely from the target hidden states, so it is fixed-length. Practically, For short sentences, only use the top part of $\alpha_t$; while for long sentences, ignore words near the end.

Local Attention

Local attention choose to focus on only a small subset of the source positions, for each target word. The model first generates an alignment position $p_t$ for target word at time $t$. The context vector $c_t$, thus, is derived as a weighted average over the source hidden states within the window $\left[p_t-D, p_t+D \right]$. Hence, the alignment vector $\alpha_t$ is fixed-length now.

$$p_t = \begin{cases} t, &\text{Monotonic alignment} \\ S \cdot \mathrm{sigmoid} \left( v_p^\top \tanh \left( W_p h_t \right) \right), &\text{Predictive alignment} \end{cases}$$

where $W_p$ and $v_p$ are trainable parameters, and $S$ is the source length.
To favor alignment points near $p_t$, place a Gaussian distribution centered around $p_t$. Then, the alignment weights are:

$$a_{st} = \mathrm{align} \left( \bar{h}_s, h_t \right) \cdot \exp \left( -\frac{(s-p_t)^2}{2\sigma^2} \right)$$

The standard deviation is empirically set as $\sigma = \frac{D}{2}$.

Neural Turing Machines

Graves, A., Wayne, G., & Danihelka, I. 2014. Neural Turing machines. arXiv preprint arXiv:1410.5401.

An alternative of alignment function named content-based addressing:

$$\mathrm{score} \left( \bar{h}_s, h_t \right) = \mathrm{cosine} \left( \bar{h}_s, h_t \right)$$

An Survey on Attention in NLP

Hu, D. 2019. An introductory survey on attention mechanisms in NLP problems. In Proceedings of SAI Intelligent Systems Conference (pp. 432-448). Springer, Cham.

An alternative of alignment function based on MLP:

$$\mathrm{score} \left( \bar{h}_s, h_t \right) = \sigma \left( v_a^\top \tanh \left( W_a \left[ \bar{h}_s; h_t \right] + b_{a1} \right) + b_{a2} \right)$$

Memory-Based Attention

What are Qurey and Key-Value Pairs?

Given a list of key-value vector pairs $\left\{ \left( k_i, v_i \right) \right\}$ stored in memory and a query vector $q$, the attention computation follows three steps:

$$\begin{aligned} e_i &= \mathrm{score} (q, k_i), &\text{Address Memory} \\ \alpha_i &= \frac{\exp(e_i)}{\sum_k \exp(e_k)}, &\text{Normalize} \\ c &= \sum_i \alpha_i v_i, &\text{Read Contents} \end{aligned}$$

Typically, memory is simply a synonym for the source sequence. In other words, each key-value pair is aligned to a step in the source sequence. Further, the key and value are typically equal within each pair (e.g., both are the encoder’s hidden state), and this reduces to the basic attention mechanism.
The query vector is distinct in different NLP tasks. For example, in language translation, the query is the decoder’s last hidden state; in question-answering system, the query is the embedding of question.

Attention is All You Need

Vaswani, A., Shazeer, N., Parmar, N., et al. 2017. Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008).

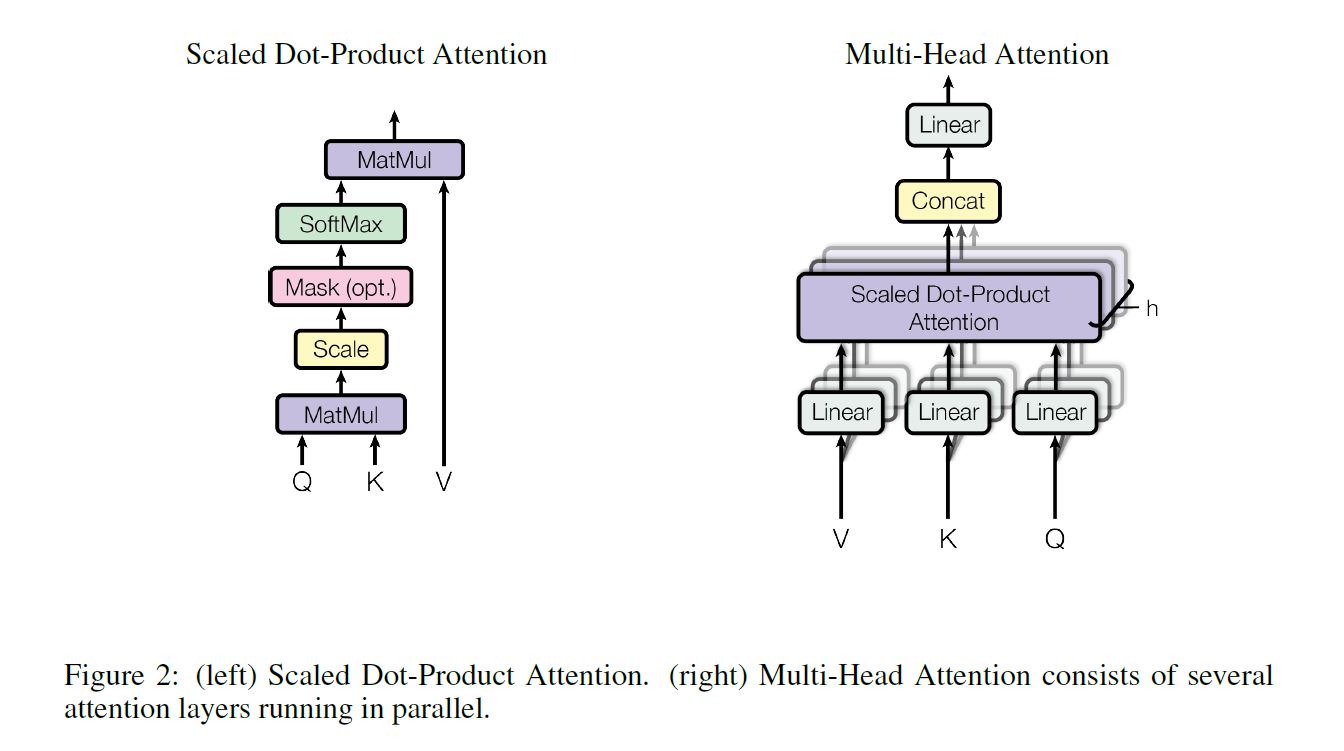
Scaled Dot-Product Attention

An attention function can be described as mapping a query and a set of key-value pairs to an output (i.e., context vector). The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function (i.e., normalized alighment function) of the query with the corresponding key.

Assume the queries and keys are of dimension $d_k$, and values are of dimension $d_v$, the alighment function is:

$$\mathrm{score} (q, k) = \frac{q^\top k}{\sqrt{d_k}}$$

where $q$ and $k$ are query and key vectors. It is idential to the dot-product attention, expect for the scaling factor $\frac{1}{\sqrt{d_k}}$.
In practice, pack the queries, keys and values into matrices:

• Quries: A matrix $Q \in \Bbb{R}^{N_q \times d_k}$;
• Keys: A matrix $K \in \Bbb{R}^{N_k \times d_k}$;
• Values: A matrix $V \in \Bbb{R}^{N_k \times d_v}$.

And the full attentioned values (context vectors) are computed by:

$$\mathrm{Attention}(Q, K, V) = \mathrm{softmax}\left( \frac{QK^\top}{\sqrt{d_k}} \right) V$$

Multi-Head Attention

In the single-head scenario, the attention function is performed with $d_{model}$-dimensional queries, keys and values. (e.g., the queries, keys and values are all $d_{model}$-dimensional embeddings).
In the multi-head scenario:

• Project the $d_{model}$-dimensional queries, keys and values to $d_k$, $d_k$ and $d_v$ dimensions, for $h$ times, resulting in $h$ versions of projected queries, keys and values.
• For each version, perform attention function on the projected queries, keys and values, yielding $h$ versions of $d_v$-dimensional attentioned values.
• Concatenate the $h$ versions of attentioned values and then futher project the concatenated attentioned values to $d_{model}$ dimension.

Formerly,

$$\begin{aligned} \mathrm{MultiHead}(Q, K, V) &= \mathrm{Concat}(head_1, \dots, head_h) W^O \\ \text{where } head_i &= \mathrm{Attention} \left( Q W_i^Q, K W_i^K, V W_i^V \right) \end{aligned}$$

where $W_i^Q \in \Bbb{R}^{d_{model} \times d_k}$, $W_i^K \in \Bbb{R}^{d_{model} \times d_k}$, $W_i^V \in \Bbb{R}^{d_{model} \times d_v}$ and $W^O \in \Bbb{R}^{hd_v \times d_{model}}$ are trainable parameter matrices.

Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. While with a single attention head, averaging inhibits this.

Application of Attention in Transformer

The Transformer uses multi-head attention in three different ways:

• Encoder-Decoder Attention layers
  • Queries come from the output of the previous decoder layer
  • Memory keys and values come from the output of the encoder
  • This mimics the typical Encoder-Decoder attention mechanisms in Seq2Seq models
• Self-Attention layers in the encoder
  • All the queries, keys and values come from the output of the previous encoder layer
  • Each position can attend to all positions in the previous layer
• Self-Attention layers in the decoder
  • All the queries, keys and values come from the output of the previous decoder layer
  • Each position attends to positions up to and including that position in the previous layer (The target sequence is right shifted by one position)
  • Mask out (setting to $-\infty$) all values in the input of the softmax which correspond to illegal connections

Self-Attention

Self-attention is a new scheme, other than RNN and CNN, used for mapping a variable-length sequence of representations $\left(x_1, x_2, \dots, x_n\right)$ to another sequence of equal length $\left(z_1, z_2, \dots, z_n\right)$, with $x_i, z_i \in \Bbb{R}^d$.

Layer Type	Complexity per Layer	Sequential Operations	Max Path Length
Self-Attention	$O(n^2 \cdot d)$	$O(1)$	$O(1)$
RNN	$O(n \cdot d^2)$	$O(n)$	$O(n)$
CNN	$O(k \cdot n \cdot d^2)$	$O(1)$	$O(\log_k(n))$
Self-Attention (Restricted)	$O(r \cdot n \cdot d)$	$O(1)$	$O(n/r)$