西瓜书笔记：模型评估与选择（第 2 章）

过拟合，经验误差，评估方法，性能度量等。

经验误差与过拟合

经验误差
过拟合

评估方法

留出法
Cross-Validation
自助法（Bootstrapping）：平均 36.8% 的样本在采样集外，可用于包外估计（Out-of-Bag Estimate）。

性能度量

回归任务：Mean Square Error
分类任务：Accuracy

Precision 和 Recall

Precision 和 Recall 的定义

$\begin{aligned} Precision =& \frac {N_{TruePos}} {N_{PredPos}} = \frac {N_{TruePos}} {N_{TruePos} + N_{FalsePos}} \\ Recall =& \frac {N_{TruePos}} {N_{OriPos}} = \frac {N_{TruePos}} {N_{TruePos} + N_{FalseNeg}} \end{aligned}$

F1-score 是 Precision 和 Recall 的调和平均数

$F1 = \left( \frac {P^{-1} + R^{-1}} {2} \right)^{-1} = \frac {2}{1/P + 1/R}$

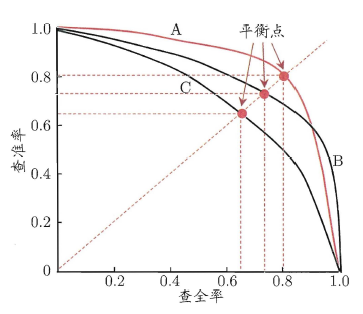
P-R 曲线

当判别为正例的标准最严格（仅有极少数最明显的被判别为正例），此时 $Recall \to 0$，$Precision \to 1$。
当判别为正例的标准最宽松（所有样本均判别为正例），此时 $Recall \to 1$，$Precision \to N_{OriPos} / N$。
Precision 应该不会趋近于 0 吧？

ROC 和 AUC

ROC 曲线

ROC 全称受试者工作特征（Receiver Operating Characteristics），该曲线横轴为假正例率（False Positive Rate, FPR），纵轴为真正例率（True Positive Rate,TPR），定义为

$\begin{aligned} {\it FPR} =& \frac {N_{FalsePos}} {N_{OriNeg}} \\ {\it TPR} =& \frac {N_{TruePos}} {N_{OriPos}} = Recall \end{aligned}$

当判别为正例的标准最严格（仅有极少数最明显的被判别为正例），此时 ${\it TPR} \to 0$，${\it FPR} \to 0$。
当判别为正例的标准最宽松（所有样本均判别为正例），此时 ${\it TPR} \to 1$，${\it FPR} \to 1$。

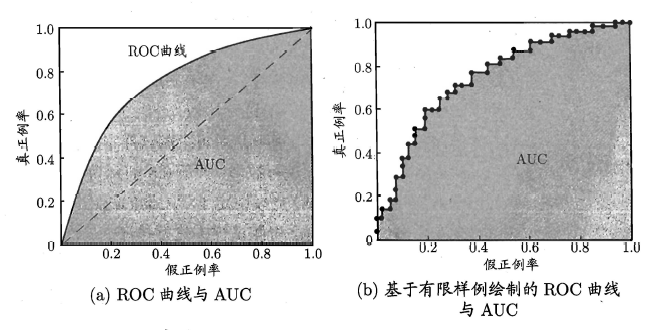
AUC （Area under ROC Curve）就是 ROC 曲线下的面积，可以作为模型性能指标。
K-S 指标：${\it KS} = \max {\it TPR} - {\it FPR}$

在风险管理中，假正例的成本远高于假反例，因此需要更关注提高 Precision （或者说降低 FPR），而 Recall （或者 TPR）的权重更小。

方差与偏差

模型的 泛化误差 可以分解为偏差、方差、噪声之和。
以回归任务为例，对测试样本 ${\pmb x}$，令 $y_D$ 为 ${\pmb x}$ 在整个数据集中的标记，$y$ 为 ${\pmb x}$ 的真实标记，则噪声为

$\varepsilon^2 = \mathbb{E}_D [(y_D-y)^2]$

$f({\pmb x}; D)$ 为训练集 $D$ 上学得的模型 $f$ 在 ${\pmb x}$ 上的预测输出。在潜在的不同训练集 $D$ 上训练得到的学习算法的 期望预测 为

$\bar{f}({\pmb x}) = \mathbb{E}_D [f({\pmb x}; D)]$

因此，使用不同训练集产生的方差为

$var({\pmb x}) = \mathbb{E}_D [(f({\pmb x}; D) - \bar{f}({\pmb x}))^2]$

期望预测 与真实标记的差别偏差为

$bias^2({\pmb x}) = (\bar{f}({\pmb x}) - y)^2$

对算法的 期望泛化误差 进行分解

$\begin{aligned} \mathbb{E}_D [(f({\pmb x}; D) - y_D)^2] =& \mathbb{E}_D [(f({\pmb x}; D) - \bar{f}({\pmb x}) + \bar{f}({\pmb x}) - y_D)^2] \\ =& \mathbb{E}_D [(f({\pmb x}; D) - \bar{f}({\pmb x}))^2] + \mathbb{E}_D [(\bar{f}({\pmb x}) - y_D)^2] + \underbrace{ \mathbb{E}_D [ 2 (f({\pmb x}; D) - \bar{f}({\pmb x}))(\bar{f}({\pmb x}) - y_D) ]}_{=0, \, \text{because of independence}} \\ =& var({\pmb x}) + \mathbb{E}_D [(\bar{f}({\pmb x}) - y + y - y_D)^2] \\ =& var({\pmb x}) + (\bar{f}({\pmb x}) - y)^2 + \mathbb{E}_D [(y - y_D)^2] + \underbrace{ \mathbb{E}_D [ 2 (\bar{f}({\pmb x}) - y)(y - y_D) ]}_{=0, \, \text{because of independence}} \\ =& var({\pmb x}) + bias^2({\pmb x}) + \varepsilon^2 \end{aligned}$

对方差与偏差的理解：

过拟合：不同训练集 $D$ 产生的预测 $f({\pmb x}; D)$ 之间差异大，也就是 方差大。
欠拟合：训练集未能使得模型 $f({\pmb x}; D)$ 显著变化，也就是 偏差大。