《线性代数的本质》笔记

3Blue1Brown 视频《线性代数的本质》（bilibili, YouTube）的笔记。用于构建线性代数的几何直觉。

向量

• 不同学科视角下的 向量

  • 物理学视角：箭头（长度 + 方向）决定一个向量，向量平移不变
  • 计算机学视角：向量等同于有序的数字 列表
  • 数学视角：向量是任意支持符合向量计算规则（加法和乘法）的对象

• 如果把向量的起点默认为原点，就能将 箭头 和 列表 两种视角相统一

  • 向量加法
    • 箭头视角：把向量依次首尾相连
    • 列表视角：把向量各元素分别加总
  • 向量乘以标量（Scalar）
    • 箭头视角：缩放（Scaling）
    • 列表视角：把向量各元素分别乘以标量，分别缩放

定义基向量（Basis Vectors）

$${\pmb i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \; {\pmb j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$$

把向量看成是基向量的 缩放后相加 的结果，例如

$$\begin{bmatrix} 3 \\ -2 \end{bmatrix} = 3 {\pmb i} -2 {\pmb j}$$

我们完全可以使用不同的基向量。因此，当我们使用数字列表表示向量时，实际的向量总是依赖于我们所采用的基向量。

这种向量的 缩放后相加 实际上就是 线性组合（Linear Combination）。也就是说，向量可以理解成基向量的线性组合。

一组基向量的线性组合所能到达的点的集合就是该组基向量张成的 空间（Span）。在二维情况下，只要基向量不共线，它们张成的空间就覆盖平面上所有的点；如果基向量共线，它们张成的空间就只有一条线；如果基向量都是零向量，它们张成的空间就只有一个点。

如果能从基向量中移除一个向量，而不影响它们张成的空间，就说这组基向量是 线性相关（Linearly Dependent）；否则就是 线性无关（Linearly Independent）。

矩阵乘以向量

线性变换（Linear Transformation）：变换 就是函数的另一种说法，线性变换就是向量到向量的映射；变换 一词暗示了是输入向量 移动 到输出向量的位置。

在 线性变换 中，只要确定基向量的变换后位置，就能确定其他所有向量的变换后位置。如果

$${\pmb v} = \begin{bmatrix} x \\ y \end{bmatrix} = x \left( {\pmb i} \right) + y \left( {\pmb j} \right)$$

那么，在变换后有

$${\pmb v'} = x \left( {\pmb i'} \right) + y \left( {\pmb j'} \right)$$

举个例子，假设在变换后有

$${\pmb i'} = \begin{bmatrix} 1 \\ -2 \end{bmatrix}, \; {\pmb j'} = \begin{bmatrix} 3 \\ 0 \end{bmatrix}$$

就有

$$\begin{aligned} {\pmb v'} =& x \left( {\pmb i'} \right) + y \left( {\pmb j'} \right) \\ =& x \begin{bmatrix} 1 \\ -2 \end{bmatrix} + y \begin{bmatrix} 3 \\ 0 \end{bmatrix} \\ =& \begin{bmatrix} x+3y \\ -2x \end{bmatrix} \end{aligned}$$

把基向量变换后的向量作为列排成 2*2 的矩阵 $\begin{bmatrix} 1 & 3 \\\\ -2 & 0 \end{bmatrix}$，此时矩阵乘以向量 ${\pmb v} = \begin{bmatrix} x \\\\ y \end{bmatrix}$，就是

$$\begin{bmatrix} 1 & 3 \\ -2 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x+3y \\ -2x \end{bmatrix} = {\pmb v'}$$

也就是在求变换后的 ${\pmb v}$。

所以，矩阵中的各列依次代表线性变换中，各基向量在变换后的结果（位置），也就是 列向量。如果说，向量是基向量的线性组合，那么，矩阵乘以向量的结果可以理解成，线性变换之后的基向量的线性组合。

整体上，矩阵对应的线性变换将 原基向量张成的空间 映射到 变换后基向量张成的空间。如果矩阵的各列是线性相关的，说明在线性变换后，基向量是共线的。在二维的情况下，就是将平面压缩成一维直线。

矩阵乘以矩阵

依次两个线性变换称为 复合变换（Composition of Transformations）。
一个向量依次经历两个矩阵的线性变换得到的结果，等价于其经过一个复合变换的结果，例如

$$\underbrace{\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}}_{\text{Shear}} \left( \underbrace{\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}}_{\text{Rotation}} \begin{bmatrix} x \\ y \end{bmatrix} \right) = \underbrace{\begin{bmatrix} 1 & -1 \\ 1 & 0 \end{bmatrix}}_{\text{Composition}} \begin{bmatrix} x \\ y \end{bmatrix}$$

那么，可以定义矩阵的乘法

$$\underbrace{\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}}_{\text{Shear}} \underbrace{\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}}_{\text{Rotation}} = \underbrace{\begin{bmatrix} 1 & -1 \\ 1 & 0 \end{bmatrix}}_{\text{Composition}}$$

注意，如果将矩阵的乘法看成是两个相继的线性变换，则需要 从右往左 阅读，即被作用的向量是先经历靠右矩阵的变换，然后经历靠左矩阵的变换。这类似函数的嵌套，即 $f \left( g(x) \right)$。

我们来追踪一下基向量的变换过程，以 ${\pmb i}$ 为例。经历第一个矩阵的变换后，该基向量变成 $\begin{bmatrix} 0 \\\\ 1 \end{bmatrix}$ （即右侧矩阵的第一列）。经历第二个矩阵的变换后，该基向量进一步变成 $\begin{bmatrix} 1 & 1 \\\\ 0 & 1 \end{bmatrix} \begin{bmatrix} 0 \\\\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\\\ 1 \end{bmatrix}$，正好是复合矩阵的第一列。

行列式

行列式（Determinant）是线性变换后相比变换前空间中体积（二维情况下的面积）的缩放比例（Scaling Factor）。
如果变换改变了空间的定向（Orientation），那么行列式就是 负值。对二维平面而言，改变定向类似“翻转平面”；对三维空间而言，改变定向意味着是否符合“右手定则”。

行列式的计算：

$$\det \left( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right) = ad - bc$$

如果矩阵的行列式等于 零，则意味着原空间经过该线性变换后，被压缩到一个低维空间里，使得“体积”变为零。同时，这也意味着变换后的基向量是 线性相关 的。

线性方程组

线性方程组（Linear System of Equations）

$$\overbrace{\begin{bmatrix} 2 & 5 & 3 \\ 4 & 0 & 8 \\ 1 & 3 & 0 \end{bmatrix}}^{\pmb A} \overbrace{\begin{bmatrix} x \\ y \\ z \end{bmatrix}}^{\pmb x} = \overbrace{\begin{bmatrix} -3 \\ 0 \\ 2 \end{bmatrix}}^{\pmb v}$$

这相当于在问：什么向量 ${\pmb x}$ 经过变换 ${\pmb A}$ 后，能得到向量 ${\pmb v}$？
从几何直观出发，如果 ${\pmb A}$ 的行列式不为零，则有一个 逆变换（Inverse Transformation） ${\pmb A}^{-1}$，有

$${\pmb x} = {\pmb A}^{-1} {\pmb v}$$

如果 ${\pmb A}$ 的行列式为零，该矩阵将原空间压缩到一个低维空间里，则不存在逆变换，因为不存在一个“函数”，可以将一个值映射到多个值。
如果 ${\pmb A}$ 的行列式为零，只有当 ${\pmb v}$ 恰好处在那个被压缩后的低维空间里，原方程组才有解（且有无穷多个解），否则没有解。

秩（Rank）是矩阵对应的 线性变换的输出空间的维度。这里，输出空间其实就是矩阵的每一列作为向量所张成的空间，被称为 列空间（Column Space）。一个矩阵的秩的最大可能取值就是其列数，只有取到该最大值时，行列式才不为零，此时被称为 满秩（Full Rank）；当秩小于列数时，行列式为零。

当矩阵满秩时，只有零向量会被映射为零向量。当矩阵不满秩时，意味着有些非零向量被映射成零向量，这些原空间中的非零向量张成的空间被称为 零空间（Null Space）或者 核（Kernel）。当 ${\pmb v}$ 正好是零向量时，零空间中的所有向量构成原方程组的解集。

非方阵

非方阵（Non-Square Matrix）是不同维度的空间之间的线性变换，从 列数维度 的空间映射到 行数维度 的空间（但不一定能够“充满”、“张成”该空间），矩阵中的各 列向量 依然代表线性变换后的基向量，张成 列空间。

一个3*2（3行2列）的矩阵，就是从一个2维空间映射到3维空间，但显然不能张成该3维空间；通常只能张成一个平面，也可能压缩成直线或原点。

一个2*3（2行3列）的矩阵，就是从一个3维空间映射到2维空间，通常能够张成该2维空间，也可能压缩成直线或原点。

点积

${\pmb v}$ 和 ${\pmb w}$ 的点积，在几何上等价于先将 ${\pmb w}$ 投影（Project）到 ${\pmb v}$ 的方向上，然后投影得到的长度乘以 ${\pmb v}$ 的长度。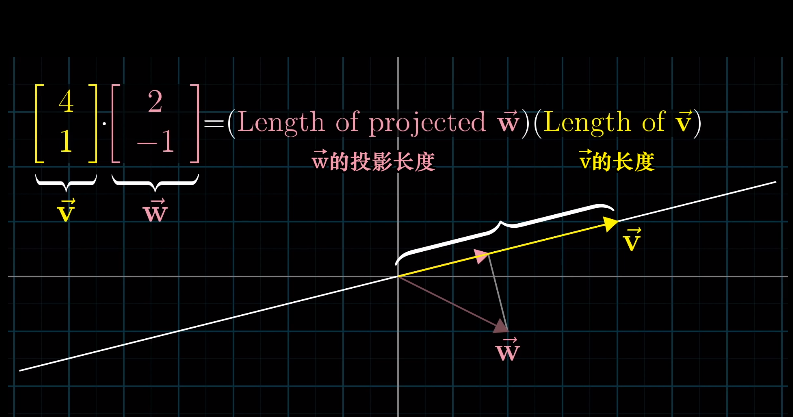

$${\pmb v} \cdot {\pmb w} = \Vert {\pmb v} \Vert \Vert {\pmb w} \Vert \cos \theta$$

代数的计算方法：

$${\pmb v} \cdot {\pmb w} = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \cdot \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} = v_1 w_1 + v_2 w_2 = \begin{bmatrix} v_1 & v_2 \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \end{bmatrix}$$

可以把向量 ${\pmb v}$ 看成一个1*2的矩阵，该矩阵代表了一个线性变换，该线性变换将一个2维空间映射为1维空间，那么 $[v_1]$ 代表第一个基向量映射后的位置，$[v_2]$ 代表第二个基向量映射后的位置，向量 ${\pmb w} = \begin{bmatrix} w_1 \\\\ w_2 \end{bmatrix}$ 映射后的位置就是 $w_1 [v_1] + w_2 [v_2]$，即 $w_1 v_1 + w_2 v_2$。

在以上过程中，2维空间映射为1维空间其实就是 投影 的过程。

所以，向量也可以理解成一个1行多列的矩阵，对应一个线性变换。任意一个其他向量经过该线性变换得到的结果，就是两个向量的点积。

叉积

${\pmb v}$ 和 ${\pmb w}$ 的叉积，在几何上是向量张成的平行四边形的面积（并考虑定向问题决定正负号/方向）。

对于二维空间，叉积的结果是一个数（不严格定义）：

$${\pmb v} \times {\pmb w} = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \times \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} = \det \left( \begin{bmatrix} v_1 & w_1 \\ v_2 & w_2 \end{bmatrix} \right) = v_1 w_2 - v_2 w_1$$

对于三维空间，叉积的结果是一个向量：

$${\pmb v} \times {\pmb w} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} \times \begin{bmatrix} w_1 \\ w_2 \\ w_3 \end{bmatrix} = \det \left( \begin{bmatrix} {\pmb i} & v_1 & w_1 \\ {\pmb j} & v_2 & w_2 \\ {\pmb k} & v_3 & w_3 \end{bmatrix} \right)$$

该向量垂直于 ${\pmb v}$ 和 ${\pmb w}$ 张成的平面，方向根据右手定则确定，长度等于 ${\pmb v}$ 和 ${\pmb w}$ 张成的面积。

在几何上，叉积的含义是：如果一个向量 ${\pmb p} = \begin{bmatrix} p_1 \\\\ p_2 \\\\ p_3 \end{bmatrix}$ 与任意向量 ${\pmb x} = \begin{bmatrix} x \\\\ y \\\\ z \end{bmatrix}$ 的点积等于由 ${\pmb x}$、${\pmb v}$ 和 ${\pmb w}$ 排成的矩阵的行列式，那么这个向量 ${\pmb p}$ 是多少？即

$$\begin{bmatrix} p_1 \\ p_2 \\ p_3 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \det \left( \begin{bmatrix} x & v_1 & w_1 \\ y & v_2 & w_2 \\ z & v_3 & w_3 \end{bmatrix} \right)$$

向量 ${\pmb p}$ 就是 ${\pmb v}$ 和 ${\pmb w}$ 的叉积。

实际上，由 ${\pmb x}$、${\pmb v}$ 和 ${\pmb w}$ 排成的矩阵的行列式是一个将 ${\pmb x}$ 从3维空间映射到1维空间的线性变换；既然是线性变换，就一定存在一个向量 ${\pmb p}$ 与之对应。

基变换

当我们采用 ${\pmb i}$ 和 ${\pmb j}$ 作为基向量，意味着在对应的 坐标系（Coordinate System）下定义它们的 坐标（Coordinates）依次为 $\begin{bmatrix} 1 \\\\ 0 \end{bmatrix}$ 和 $\begin{bmatrix} 0 \\\\ 1 \end{bmatrix}$。

如果我们换一组向量作为基向量呢？比如，我们把向量 $2{\pmb i}+{\pmb j}$ 和 $-{\pmb i}+{\pmb j}$ 分别作为新的基向量，由此定义了一个 新坐标系，在这一 新坐标系 下，$2{\pmb i}+{\pmb j}$ 和 $-{\pmb i}+{\pmb j}$ 的坐标也依次定义为 $\begin{bmatrix} 1 \\\\ 0 \end{bmatrix}$ 和 $\begin{bmatrix} 0 \\\\ 1 \end{bmatrix}$。但显然，这两个向量在 原坐标系 中的坐标为 $\begin{bmatrix} 2 \\\\ 1 \end{bmatrix}$ 和 $\begin{bmatrix} -1 \\\\ 1 \end{bmatrix}$。

不同的基向量意味着不同的坐标系，不同的坐标系下，我们描述同一个 向量（Vector）所采用的 坐标（Coordinates）是不同的。事实上，空间本身并没有内蕴的（Intrinsic）坐标系，并不存在绝对的基向量选择；一开始的 ${\pmb i}$ 和 ${\pmb j}$ 其实也是任意选取的。

如何在不同坐标系下进行变换（Translate）？例如，在新坐标系下的坐标 $\begin{bmatrix} x \\\\ y \end{bmatrix}$ 对应的向量，在原坐标系下的坐标是多少？

$$\begin{bmatrix} 2 & -1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = x \begin{bmatrix} 2 \\ 1 \end{bmatrix} + y \begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} 2x-y \\ x+y \end{bmatrix}$$

矩阵 $\begin{bmatrix} 2 & -1 \\\\ 1 & 1 \end{bmatrix}$ 是用 原坐标系的基向量 下的坐标来描述 新坐标系的基向量，却可以用来将 新坐标系下的坐标 转换为 原坐标系下的坐标。类似地，逆矩阵的定义和作用完全相反。

基变换与线性变换

此时，再回头看矩阵所代表的线性变换，之前的描述是 矩阵的各列依次代表变换后的各基向量。但更为精确的描述可以是，矩阵的各列依次代表变换后的各基向量的坐标。

• 区分线性变换和基变换
  • 线性变换中，基向量（坐标系）只有一组，变化的是向量。
  • 基变换中，向量不变，但需要在不同的基向量（坐标系）下描述该向量的坐标。

如果在 原坐标系 下发生了线性变换 $\begin{bmatrix} 0 & -1 \\\\ 1 & 0 \end{bmatrix}$，那么这个变换在 新坐标系 下该如何描述？
首先，对于 新坐标系 下的任意向量 ${\pmb v}$，先“翻译”到 原坐标系，即

$$\begin{bmatrix} 2 & -1 \\ 1 & 1 \end{bmatrix} {\pmb v}$$

然后，经过 原坐标系 下发生的线性变换，即

$$\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 2 & -1 \\ 1 & 1 \end{bmatrix} {\pmb v}$$

最后，将结果“翻译”回 新坐标系，即

$$\begin{bmatrix} 2 & -1 \\ 1 & 1 \end{bmatrix}^{-1} \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 2 & -1 \\ 1 & 1 \end{bmatrix} {\pmb v}$$

所以，新坐标系 下描述该线性变换的矩阵就是 $\begin{bmatrix} 2 & -1 \\\\ 1 & 1 \end{bmatrix}^{-1} \begin{bmatrix} 0 & -1 \\\\ 1 & 0 \end{bmatrix} \begin{bmatrix} 2 & -1 \\\\ 1 & 1 \end{bmatrix}$。

在看到类似 ${\pmb A}^{-1} {\pmb M} {\pmb A}$ 的矩阵结构时，通常中间的矩阵 ${\pmb M}$ 代表一种变换，而两侧的矩阵 ${\pmb A}$ 代表一种转移作用。其结果是，变换仍然是 ${\pmb M}$ 所代表的变换，只是切换了一种视角来看待这种变换。

特征向量与特征值

要理解 特征向量（Eigenvectors）和 特征值（Eigenvalues），需要建立在理解众多预备知识的基础上，包括线性变换、行列式、线性方程组和基变换。

在线性变换中，绝大部分向量都偏离了原来的方向，只有少部分向量仍然保留在原来的方向。对这部分向量而言，线性变换的效果相当于缩放（乘以一个标量）。这样的向量被称为 特征向量，缩放的比例就是 特征值。

$$\begin{aligned} {\pmb A} {\pmb v} =& \lambda {\pmb v} \\ {\pmb A} {\pmb v} =& \lambda I {\pmb v} \\ \left( {\pmb A} - \lambda I \right) {\pmb v} =& 0 \end{aligned}$$

由于我们希望 ${\pmb v}$ 是非零解，就意味着矩阵 $\left( {\pmb A} - \lambda I \right)$ 是不满秩的（行列式为零），即

$$\det \left( {\pmb A} - \lambda I \right) = 0$$

如果我们采用特征向量作为基向量，会怎么样？这种情况下，线性变换的效果是，每个基向量仍然保留在原来的方向上进行缩放。所以，对应的矩阵就是一个 对角矩阵（Diagnal Matrix），其对角元素就是特征值。

所以，在给定基向量（和对应的坐标系）的情况下，可以先“翻译”到特征向量作为基向量的坐标系中，进行线性变换（此时退化为每个基向量方向上的缩放变换），然后再“翻译”回原坐标系下。

假设原线性变换的矩阵是 ${\pmb M}$，存在特征向量 ${\pmb v_1}$、${\pmb v_2}$、……、${\pmb v_n}$，作为列向量排成矩阵 ${\pmb V} = \begin{bmatrix} {\pmb v_1} & {\pmb v_2} & \cdots & {\pmb v_n} \end{bmatrix}$；对应特征根 $\lambda_1$、$\lambda_2$、……、$\lambda_n$，排成对角阵 ${\pmb \Lambda} = \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\\\ 0 & \lambda_2 & \cdots & 0 \\\\ \vdots & \vdots & \ddots & \vdots \\\\ 0 & 0 & \cdots & \lambda_n \end{bmatrix}$。由上一节结论可知，从 特征向量作为基向量的坐标系 中看这个线性变换，对应的矩阵是 ${\pmb V}^{-1} {\pmb M} {\pmb V}$，该矩阵必然等于 ${\pmb \Lambda}$，即

$$\begin{aligned} {\pmb V}^{-1} {\pmb M} {\pmb V} =& {\pmb \Lambda} \\ {\pmb M} =& {\pmb V} {\pmb \Lambda} {\pmb V}^{-1} \end{aligned}$$

抽象向量空间

线性代数中最为本质的概念，行列式和特征向量等，与所选取的坐标系（基向量）是无关的。

对某种对象，如果存在某种运算，该运算满足 可加性（Additivity）和 成比例（Scaling）这两个特性，都可以被看做向量。
可加性：$L\left( {\pmb v} + {\pmb w} \right) = L\left( {\pmb v} \right) + L\left( {\pmb w} \right)$
成比例：$L\left( c {\pmb v} \right) = c L\left( {\pmb v} \right)$

对 向量 而言，线性变换 这一运算就满足可加性和成比例两个特性。
特别地，函数 也可以被看成是 向量，求导 运算对函数就满足可加性和成比例两个特性。

线性代数中的概念	应用于函数时的别名
线性变换	线性算子
点积	内积
特征向量	特征函数